Cats and Dogs for Audio: End-to-end Classification of Barks and Meows
There exist nice tutorials about learning CNNs (convolutional neural networks) out there that show how to solve simple tasks such as classification of handwritten digits or classification of cats and dogs.
Compared to the abundance of blog posts about cats and dogs classification, even a single blog post about its audio counterpart is difficult to find - not to mention that there are hardly any tutorials about deep learning applied to simple introductory tasks regarding audio.
So I had a go on a rather simple task of classifying dog sounds and cat sounds - namely, the barks and meows classification - and tried to understand and hear how it classifies barking versus meowing with a bit of auralization techniques.
Convolutional Neural Networks for Audio
Since the advent of AlexNet and successive successful models for ImageNet classification task such as VGG and ResNet, such class of neural network models called the convolutional neural networks were also used to solve tasks in different domains. Domain of speech and music was no exception. Naturally, researchers chose 2D audio features like audio spectrogram and its derivations such as mel-spectrograms, constant-Q transforms (CQT), and mel frequency cepstral coefficients (MFCC) to apply 2D convolutional kernels upon.
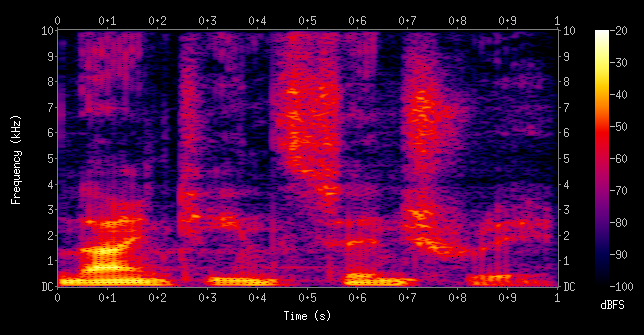
audio spectrogram (source: wikipedia)
End-to-end training
However, there have been numerous attempts to tackle the problems in an end-to-end manner, i.e., to train the CNNs by directly providing audio samples instead of once processed features. Some examples are WaveNet by van den Oord et al., which generates realistic audio samples with a sample-level autoregressive model, and SampleCNN by Lee et al., which successfully classifies multi-label tags for music.
Here is a nice three series blog posts about end-to-end deep learning for audio by Jordi Pons.
- Why do spectrogram-based VGGs suck?
- Why do spectrogram-based VGGs rock?
- What’s up with waveform-based VGGs?
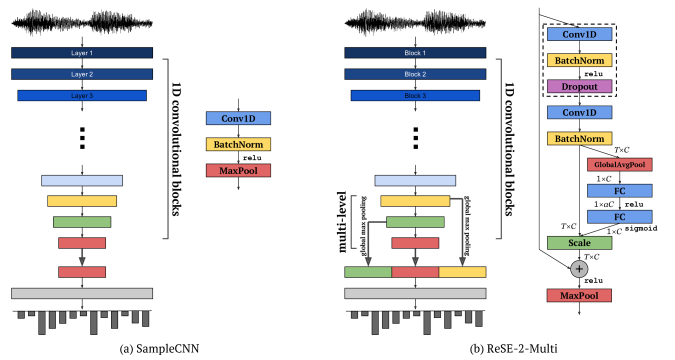
SampleCNN model architecture by Lee et al. (2017) that tags multiple labels (genre, era, etc.) to an audio excerpt
Barks vs Meows
The task of “Barks vs Meows” is fairly elementary. It is a simple binary classification between two different types of sounds: sounds of dog barking and sounds of cat meowing. One could easily formulate a logistic regression setup, but I would like to use an end-to-end CNN for the model.
The training sample data are given as ${ (x_1, y_1), (x_2, y_2), … (x_n, y_n) }$, where $x_i$ is the i-th waveform segment,
represented as an array of float valued samples,
and $y_i$ is a binary label, either 0 for meow and 1 for bark.
After training, we have to predict whether an unknown audio signal $x_q$ is a bark or a meow.
Since this is a binary classification task, we could use the binary cross-entropy loss to train the model. The loss function that the model has to minimize is thus:
\[\mathcal{L}_{BCE} = - \frac{1}{n} \sum_{i = 0}^{n} [y_i \log (x_i) + (1 - y_i) \log (1 - x_i)] \\ x_i = \sigma(z_i)\]where $\sigma$ is the sigmoid function, and $z_i$ is the logit.
These are examples of audio signals that we’re trying to classify.
meow example
bark example
Audio File Preprocessing
The dataset used to train our model is BarkMeowDB, which contains about 50 audio samples each for meows and barks, whose lengths vary from 1 second to more than 10 seconds. Since the samples have different lengths, data preprocessing is necessary to transform audio samples into input tensors that all have the same dimensions.
We would like to make the model train from a 1-second-long audio segments with sample rate 16000Hz. The preprocessing step does exactly that; it resamples each audio sample to 16000Hz and splits to 1-second-long segments, which are represented as one dimensional arrays of size 16000. During preprocessing, any split segments containing near silence are excluded.
Implementation details for the preprocessing step can be seen here.
Convolutional Neural Network with 1D Kernels
For a rather simple task of bark vs meow, a rather simple model is used. The model used to train the bark-meow classifier is a simple 5-layer CNN. However, in an end-to-end training setting, since the raw waveform input is 1-dimensional, 1D convolution layers are used instead of 2D convolution layers that are popular in the image domain. Each convolution layer has a kernel size of 3 and strides with a size of 2, in order to reduce the dimension across the time axis. In other words, the waveform gets downsampled as it goes up the layers, giving compressed, higher-level representations. At the end of each convolution layer, ReLU, batch normalization, and dropout layers follow, forming a convolution block. Therefore, each convolution block looks like:
conv_block = nn.Sequential(
nn.Conv1d(in_channels=8, out_channels=8, kernel_size=3, stride=2, bias=False),
nn.ReLU(inplace=True),
nn.BatchNorm1d(8),
nn.Dropout(p=0.5),
)
There exists a final linear classifier at the end of the convolutional network that produces inputs called ‘logits’ to the sigmoid function for the binary cross-entropy loss function.
linear_classifier = nn.Sequential(
nn.Linear(in_features=333, out_features=100),
nn.ReLU(inplace=True),
nn.Dropout(p=0.5),
nn.Linear(100, 1), # single-dimensional output = logits
)
For more implementation details, see the full implementation written in pytorch.
Training
After training 100 epochs (that took about 1 hour in my macbook pro laptop), I could get a reasonable results looking at the train and test loss graphs. Test accuracy shows about 84% for test samples.
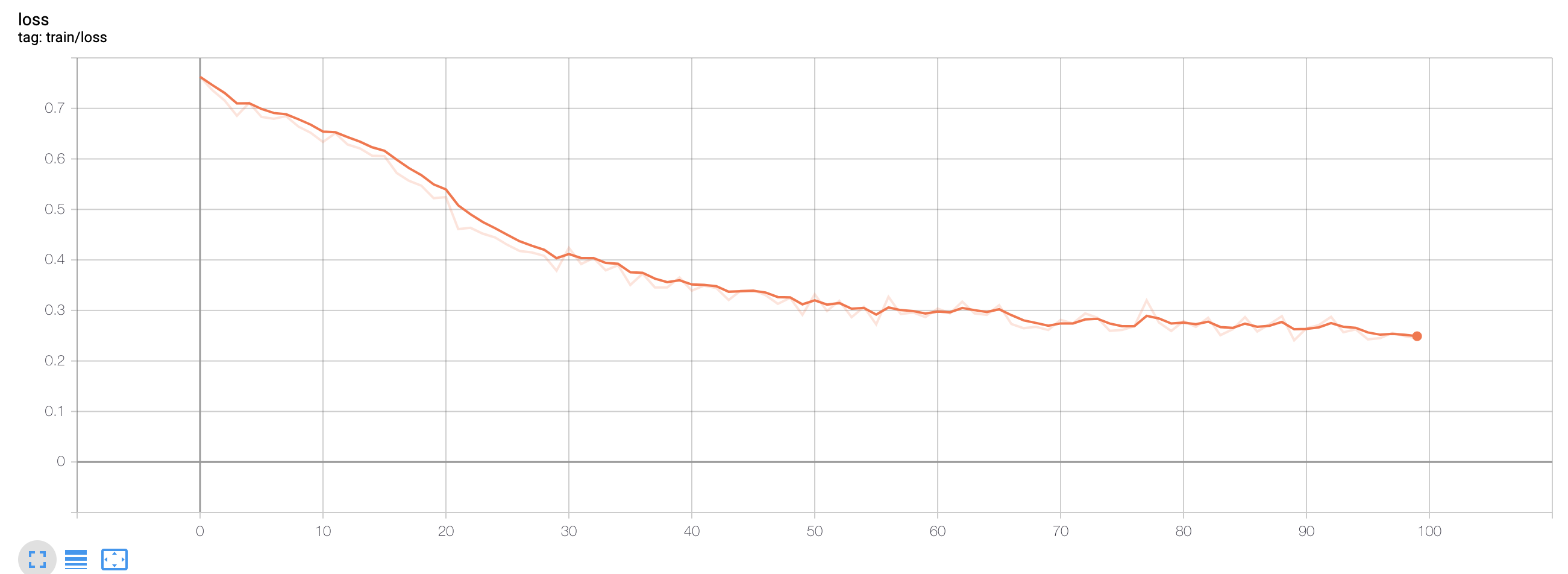
Train loss for bark-meow classifier
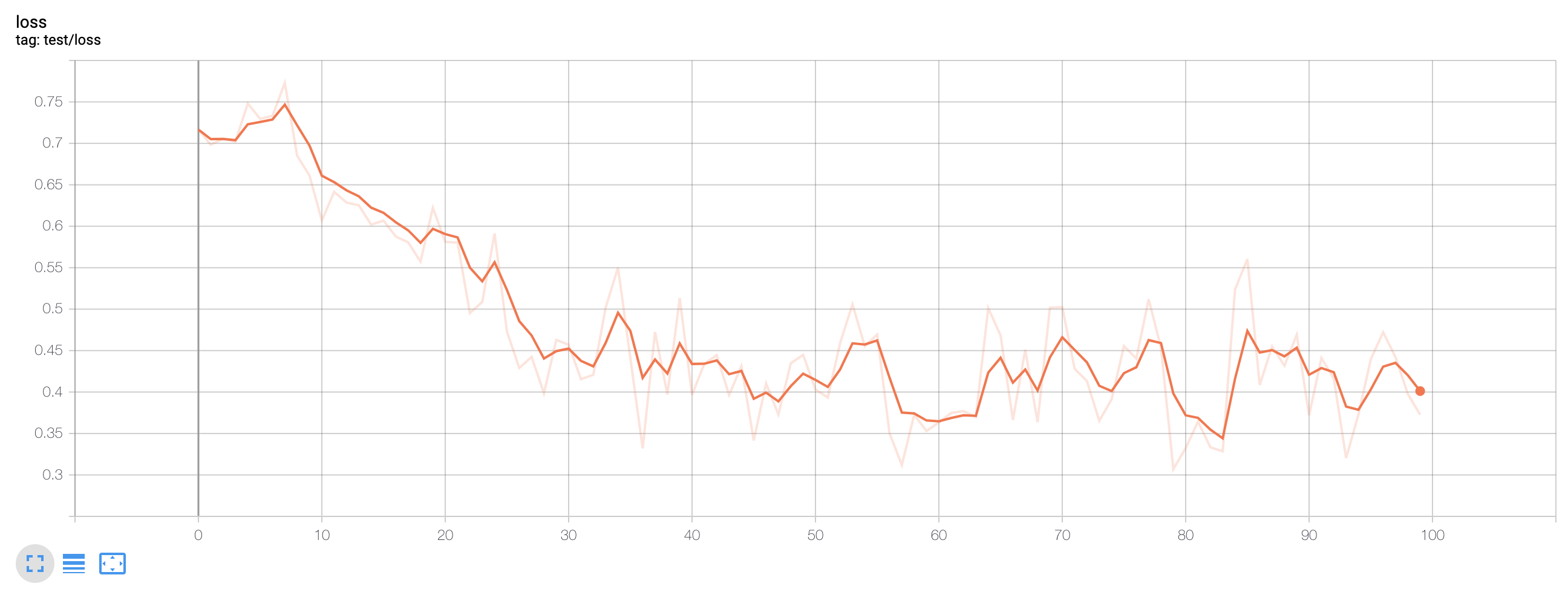
Test loss for bark-meow classifier
Auralization
We would like to gain some idea about what characteristics in the audio samples make the model decide what the label is. The technique called gradient ascent is used to produce audio clip that maximally activates the model’s kernels for a given label. That is, it helps create the most genuine bark or meow in the trained model’s perspective. We want to find the best sample $x_g$ that produces the maximum probability for label $y$.
\[\text{argmax}_{x_g} p(y | x_g)\]We add the gradient of the binary cross-entropy loss with respect to the input to the original input. We are ascending upward the probability surface by updating the inputs, hence the term gradient ascent. Starting from a randomly generated input sample $x_g$, and after iterating input updates multiple times, the resulting input segment will become the best input that produces maximum probability for the provided label.
\[x_g \leftarrow x_g + \eta \frac{\partial \mathcal{p}}{\partial x_g}\]Here are the result after 5000 iterations with learning rate $\eta = 0.001$.
Auralized Meow
meow sound auralized
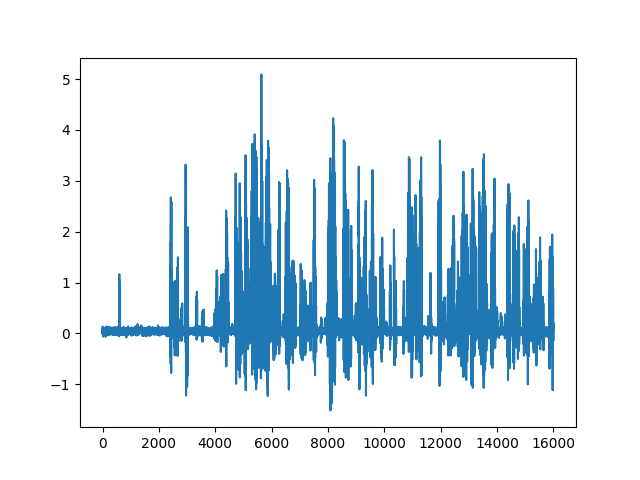
Waveform of auralized meow
Auralized Bark
bark sound auralized
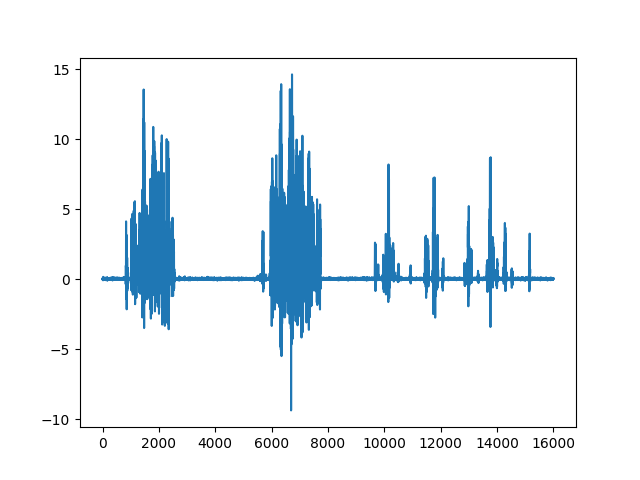
Waveform of auralized bark
Attempts to “hear” intuitions about the model’s inner workings like gradient ascent are sometimes called
auralizations,
as an audio counterpart of visualizations.
It seems apparent that the model listens to sudden magnitude bursts to predict a bark sound,
as a natural barking sound would normally distinguish from meowing sound.
On the other hand, model seems to look for long stationary sounds to predict a meow sound.
In contrast to my expectations, pitch does not seem to play a major role in prediction process,
as there are no clear differences in pitch difference in the auralized results.
Mispredictions
Here are some mispredictions the model made. These results fortify the hypothesis that the model predicts by the audio signal’s magnitude bursts. Mispredicted meowing sounds include sudden bark-like bursting sounds, and mispredicted barking sounds did not have barks-bursts but dog’s whining noise that confused the model to predict them as cat sounds.
Examples of mispredicted audio samples that are actually meows
mispredicted as dog - 1
mispredicted as dog - 2
The second example shows a man-made error where the bad timing of the split segment left only the initial burst of meow.
Examples of mispredicted audio samples that are actually barks
mispredicted as cat - 1
mispredicted as cat - 2
Conclusion
This experience of trying to apply a simple deep learning model on a bark vs. meow classification task helped gain better understanding on how end-to-end training applied on raw waveform works. Also, due to the simplicity of the task, it was easier to apply gradient ascent auralization technique, and the results gave intuitive results about how the trained model would distinguish barks versus meows. However, some fundamental questions remain unanswered from this post; can this end-to-end training give better results than training based on spectrograms?, would a trained model from spectrogram features learn to see more features other than magnitude bursts? I hope further examination and research on end-to-end learning applied on audio signals reveal more about the inner mechanisms and provide more intuition.